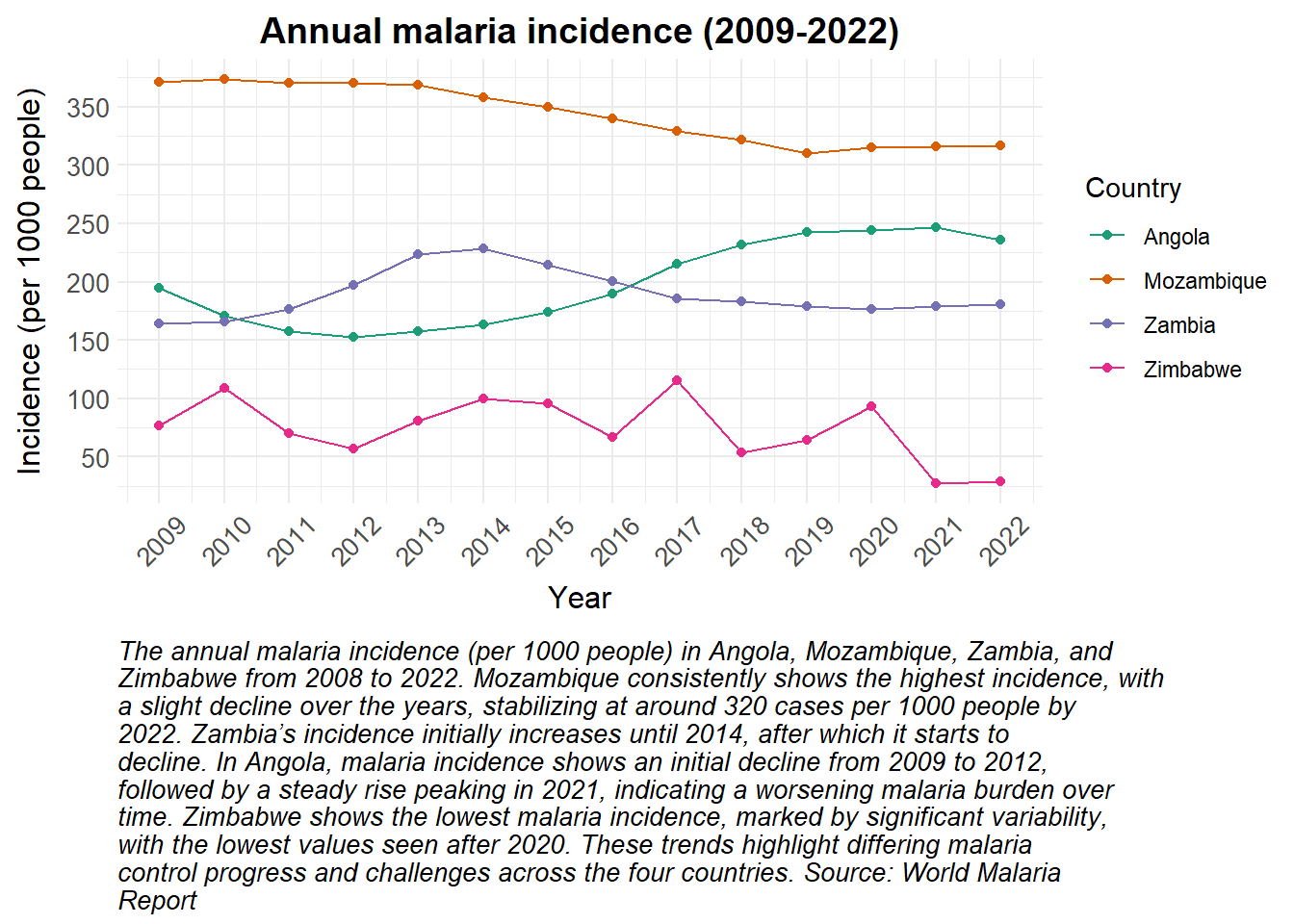
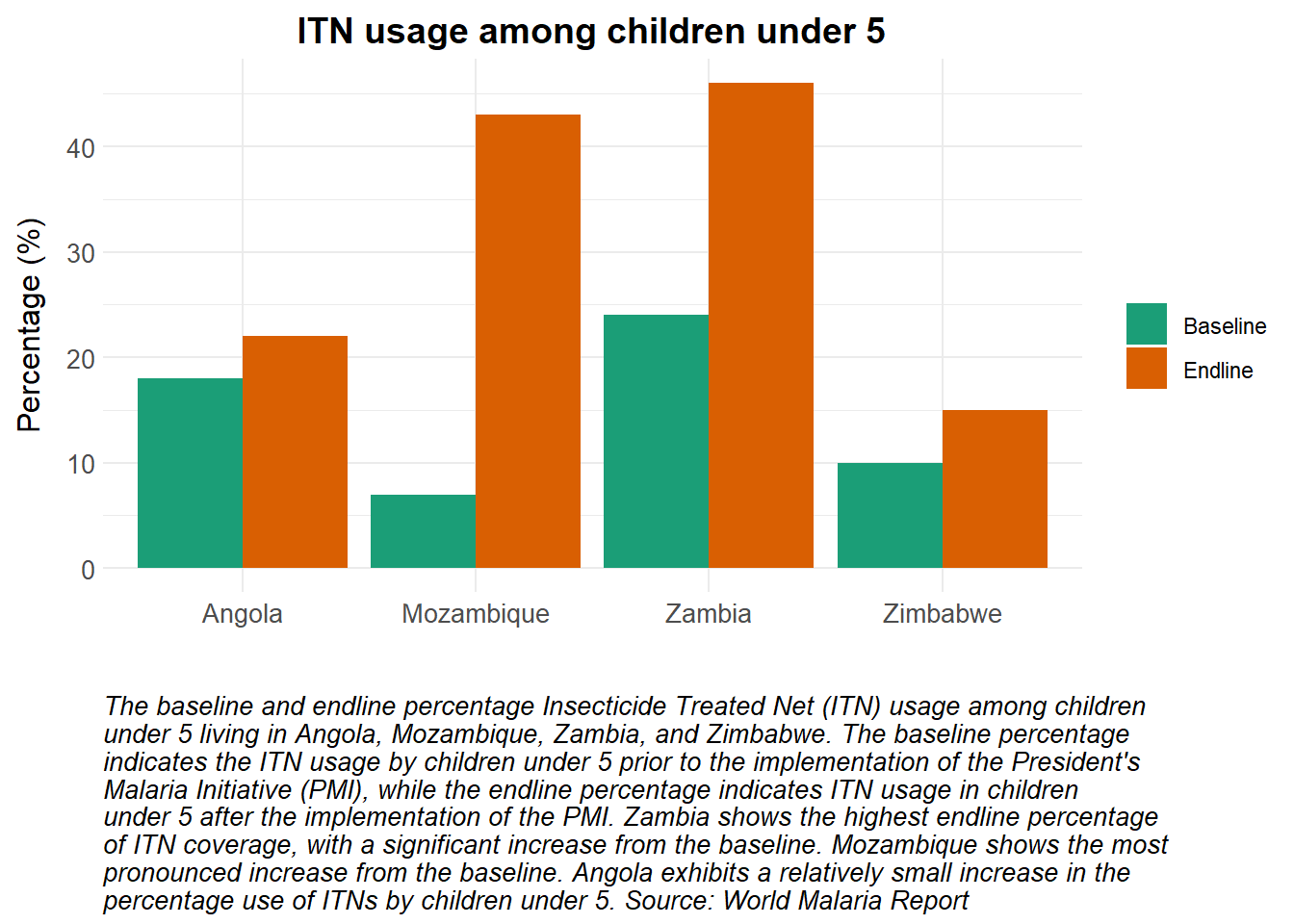
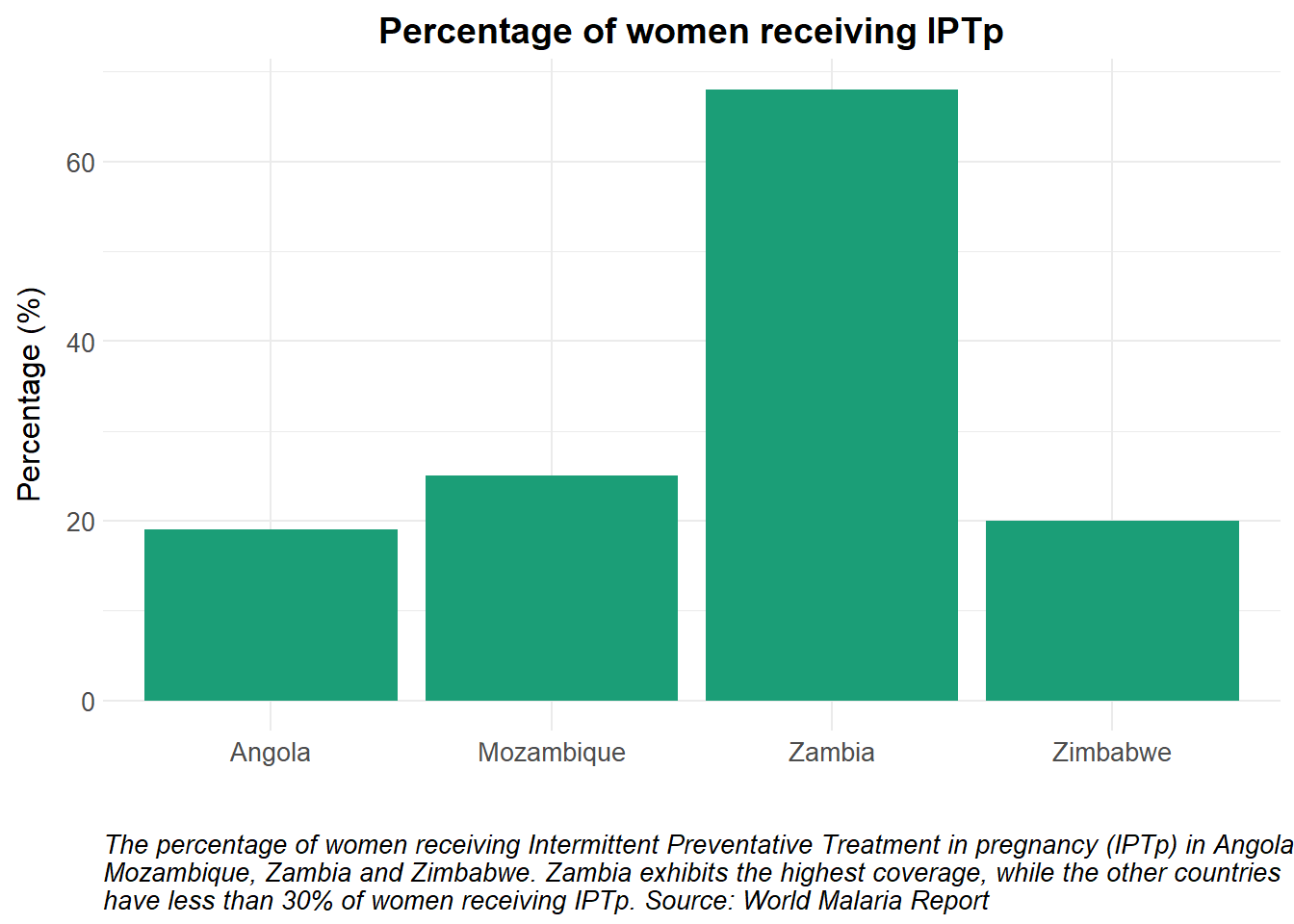
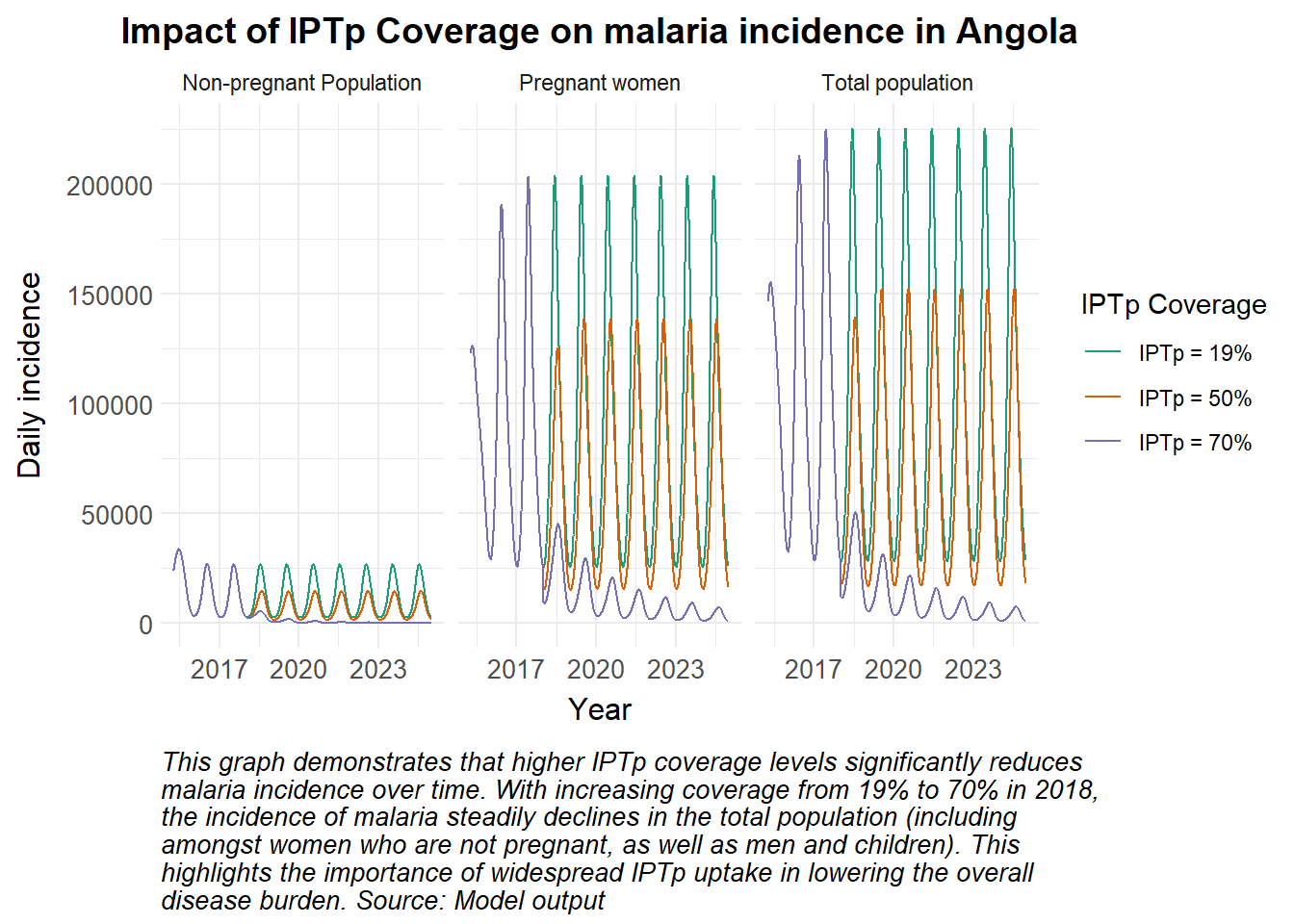
# Load packages ####
library(deSolve)
library(tidyverse)
# Time points for the simulation
Y = 10 # Years of simulation
times <- seq(0, 365*Y, 1)
# Define the SEIR-like model for malaria with time-varying IPTp coverage
iptpmodel <- function(t, x, parms) {
with(as.list(c(parms, x)), {
P = S + E + A + C + R + P_S + P_E + P_A + P_C
Infectious = C + kappa_a*A + epsilon*P_C + epsilon*kappa_a*P_A # infectious resevoir
# Seasonal forcing function
seas <- 1 * (1 + amp * cos(2 * pi * (t - phi) / 365))
# Time-dependent IPTp coverage, new coverage rates after year 5
current_iptp <- ifelse(t < (3*365), 0.19, iptp)
# Force of infection
lambda = seas*(a^2*b*c*m*Infectious/P)/(a*c*Infectious/P+mu_m)*(gamma_m/(gamma_m + mu_m))
# Pregnancy rate
omega <- f*S/(0.0002*P) # 0.02% of population are women of reproductive age
# General population
dS = mu_h*P - lambda*S - omega*S + rho*R - mu_h*S
dE = lambda*S - (gamma_h + mu_h)*E
dA = pa*gamma_h*E - (delta + mu_h)*A
dC = (1-pa)*gamma_h*E - (r + mu_h)*C
dR = delta*A + theta*delta*P_A + r*C + theta*r*P_C - (rho + mu_h)*R
# Pregnant compartments under IPTp
dP_S <- omega*S - (1-current_iptp)*lambda*P_S - mu_h*P_S
dP_E <- (1-current_iptp)*lambda*P_S - gamma_h*P_E - mu_h*P_E
dP_A <- pa*gamma_h*P_E - theta*delta*P_A - mu_h*P_A
dP_C <- (1-pa)*gamma_h*P_E - theta*r*P_C - mu_h*P_C
# Incidence and clinical cases
dGCInc = lambda*S
dPCInc = (1-current_iptp)*lambda*P_S
dTCInc = lambda*S + (1-current_iptp)*lambda*P_S
output <- c(dS, dE, dA, dC, dR, dP_S, dP_E, dP_A, dP_C, dGCInc, dPCInc, dTCInc)
list(output)
})
}
# Initial values (state variables)
start <- c(S = 15000000, # susceptible humans
E = 10000000, # exposed and infected humans
A = 7000000, # asymptomatic and infectious humans
C = 2000000, # clinical and symptomatic humans
R = 0, # recovered and semi-immune humans
P_S = 10000, # susceptible pregnant women
P_E = 4000, # exposed and infected pregnant women
P_A = 2000, # asymptomatic and infectious pregnant women
P_C = 1000, # clinical and symptomatic pregnant women
GCInc = 0, # cumulative incidence in the general population
PCInc = 0, # cumulative incidence in pregnant women
TCInc = 0 # total cumulative incidence
)
# Parameters
parms <- c(a = 0.38, # human biting rate
b = 0.3, # probability of transmission from mosquito to human
c = 0.397, # probability of transmission from human to mosquito
gamma_m = 1/10, # extrinsic incubation rate of parasite in mosquitoes
mu_m = 1/15, # birth and death rate of mosquitoes
mu_h = 1/(61*365), # birth and death rate of humans
gamma_h = 1/14, # extrinsic incubation rate of parasite in humans
pa = 0.2, # probability of asymptomatic infection
delta = 1/130, # natural recovery rate
r = 1/7, # rate of loss of infectiousness after treatment
rho = 1/160, # rate of loss of immunity after recovery
m = 3, # ratio of mosquito to human populations
kappa_a = 0.2, # relative infectiousness of asymptomatic infections
amp = 0.6, # amplitude of seasonality
phi = 186, #phase angle; start of season
epsilon = 0.75, # reduced infectiousness due to IPTp
theta = 1.25, # increased recovery rate due to IPTp
f = 5/30/365 # children born per woman over lifetime (30 reproductive years)
)
# Run model and post-processing function
run_model <- function(times, y, func, parms, scenario = "Baseline") {
mod <- ode(times = times, y = start, func = func, parms = parms)
fd <- as_tibble(as.data.frame(mod)) %>%
mutate(
P = S + E + A + C + R + P_S + P_E + P_A + P_C,
Preg = P_S + P_E + P_A + P_C,
GInc = c(0, diff(GCInc)), # New infections (Incidence)
PInc = c(0, diff(PCInc)), # New infections (Incidence)
TInc = c(0, diff(TCInc)), # New infections (Incidence)
date = as.Date("2015-01-01") + times, # Time in years
year = year(date)) %>%
pivot_longer(names_to = "variable", cols = -c(time, date, year)) %>%
mutate(scenario = scenario)
return(fd)
}
# IPTp coverage scenarios
# Baseline (19%), 50%, 70% IPTp coverage
iptp_scenarios <- c(0.19, 0.5, 0.7)
# Run the model for each IPTp scenario and store the results
results <- lapply(iptp_scenarios, function(iptp_value) {
parms["iptp"] <- iptp_value
run_model(times, start, iptpmodel, parms, scenario = paste0("IPTp = ", iptp_value * 100, "%"))
})
# Combine results for all scenarios
results_combined <- bind_rows(results)
.png)
.png)